Arrays¶
Low-Level Arrays
Compact array
Multidimensional Arrays (Matrix)
Sparse Martrix
A.1 Low-Level Arrays¶
In this section we will look at the principles behind the Python list implementation. It is important to recognize that this implementation is not going to be exactly the same as Python’s since the real list is implemented in the C programming language. The idea in this section is to use Python to demonstrate the key ideas, not to replace the C implementation!
The key to Python’s implementation of a list is to use a data type called an array common to C, C++, Java, and many other programming languages.
The array is very simple and is only capable of storing one kind of data. For example, you could have an array of integers or an array of floating point numbers, but you cannot mix the two in a single array.
The array only supports two operations: indexing and assignment to an array index.
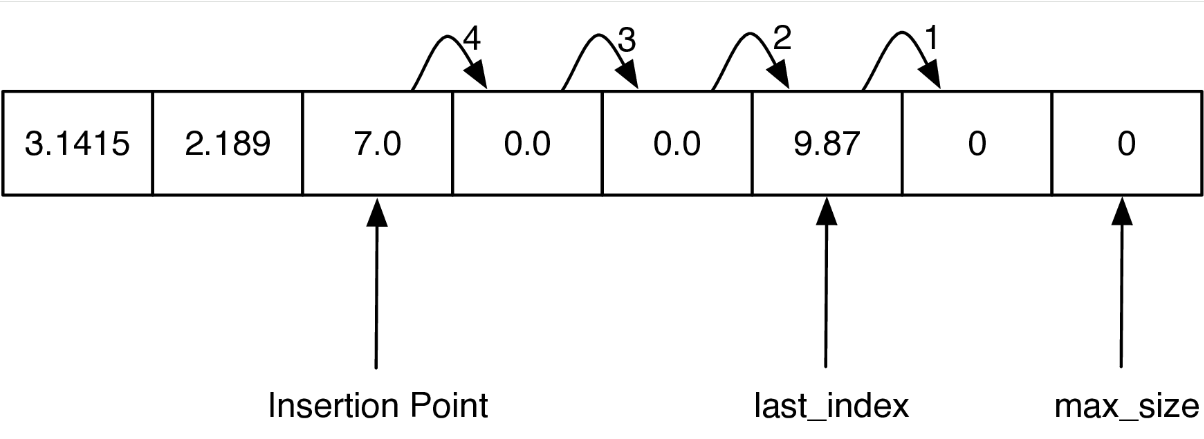
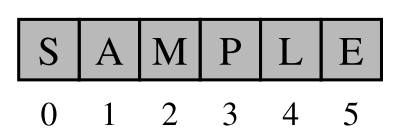
The best way to think about an array is that it is one continuous block of bytes in the computer's memory. This block is divided up into $n$-byte chunks where $n$ is based on the data type that is stored in the array. Figure below illustrates the idea of an array that is sized to hold six floating point values.

In Python, each floating point number uses 8 bytes of memory. So the array in above uses a total of 48 bytes. The base address is the location in memory where the array starts.
You have seen addresses before in Python for different objects that you have defined. For example: <__main__.Foo object at 0x5eca30> shows that the object Foo is stored at memory address 0x5eca30. The address is very important because an array implements the index operator using a very simple calculation:
item_address = base_address + index * size_of_object
For example, suppose that our array starts at location 0x000040, which is 64 in decimal. To calculate the location of the object at position 4 in the array we simply do the arithmetic:
$$64 + 4 \times 8$$
Clearly this kind of calculation is $O(1)$.
Of course this comes with some risks:
- First, since the size of an array is fixed, one cannot just add things on to the end of the array indefinitely without some serious consequences.
- Second, in some languages, like C, the bounds of the array are not even checked, so even though your array has only six elements in it, assigning a value to index 7 will not result in a runtime error!
As you might imagine this can cause big problems that are hard to track down. In the Linux operating system, accessing a value that is beyond the boundaries of an array will often produce the rather uninformative error message "segmentation fault."

The general strategy that Python uses to implement an array is as follows:
- Python uses an array that holds references (called pointers in C) to other objects (Referential Arrays).
- Python uses a strategy called over-allocation to allocate an array with space for more objects than is needed initially.
Let's look at how the strategy outlined above works for a very simple implementation. To begin, we will only implement the constructor and the append(), size() and is_empty() method. We will call this class ArrayList.
We will use a list to simulate an array:
class ArrayList:
def __init__(self, initial_capacity=8):
self._max_size = initial_capacity
self._last_index = 0
self._my_array = [None] * self._max_size
def append(self, val):
self._my_array[self._last_index] = val
self._last_index += 1
def size(self):
return self._last_index
def is_empty(self):
return self._last_index == 0
Next, let us turn to the index operators. Code below shows our Python implementation for index and assignment to an array location. Recall that the calculation required to find the memory location of the item in an array is a simple arithmetic expression.
Even languages like C hide that calculation behind a nice array index operator, so in this case the C and the Python look very much the same:
def __getitem__(self, idx):
if 0 <= idx < self._last_index:
return self._my_array[idx]
raise LookupError("index out of bounds")
def __setitem__(self, idx, val):
if 0 <= idx < self._last_index:
self._my_array[idx] = val
else:
raise LookupError("index out of bounds")
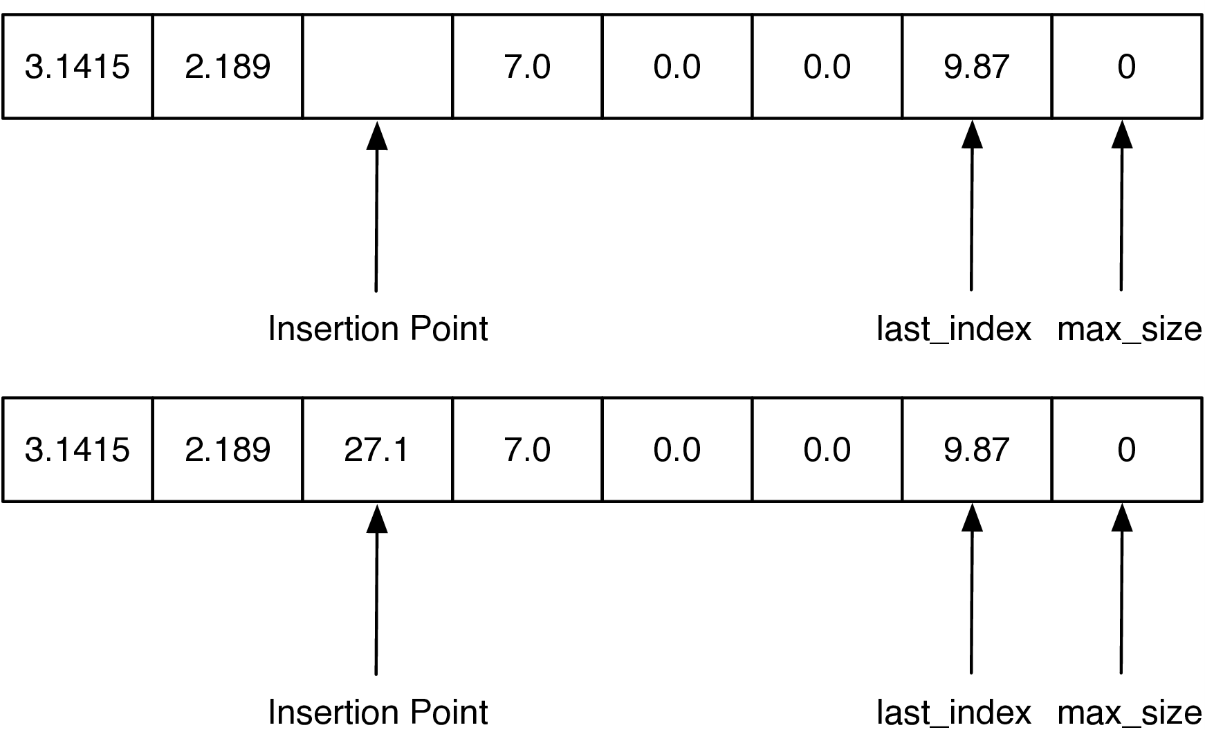
Finally, let's take a look at one of the more expensive list operations, insertion(). When we insert an item into an ArrayList we will need to first shift everything in the list at the insertion point and beyond ahead by one index position in order to make room for the item we are inserting. The process is illustrated in Figure below:
The key to implementing insert correctly is to realize that as you are shifting values in the array you do not want to overwrite any important data. The way to do this is to work from the end of the list back toward the insertion point, copying data forward.
Our implementation of insert is shown below. Note how the range is set up on line to ensure that we are copying existing data into the unused part of the array first, and then subsequent values are copied over old values that have already been shifted.
def insert(self, idx, val):
for i in range(self._last_index, idx, -1):
self._my_array[i] = self._my_array[i - 1]
self._my_array[idx] = val
self._last_index += 1
If the loop had started at the insertion point and copied that value to the next larger index position in the array, the old value would have been lost forever!
The performance of the insert is $O(n)$ since in the worst case we want to insert something at index 0 and we have to shift the entire array forward by one. On average we will only need to shift half of the array, but this is still $O(n)$.
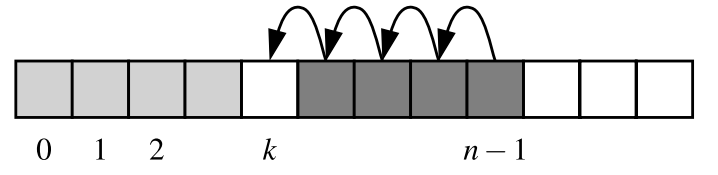
The class offers another method, named remove(), that allows the caller to specify the value that should be removed (not the index at which it resides). Formally, it removes only the first occurrence of such a value from an array, or raises an error if no such value is found.
def remove(self, val):
for i in range(self._last_index):
if self._my_array[i] == val:
for j in range(i, self._last_index - 1):
self._my_array[j] = self._my_array[j + 1]
self._my_array[self._last_index - 1] = None
self._last_index -= 1
return None
raise LookupError("value not found")
One part of the process searches from the beginning until finding the value at index k, while the rest iterates from k to the end in order to shift elements leftward. The complexity is again $O(n)$.
import sys
sys.path.append("../pythonds3/") # Change this to your actual path
from pythonds3.basic import ArrayList
my_array = ArrayList()
my_array.append(31)
my_array.append(77)
my_array.append(17)
my_array.append(93)
print(my_array, my_array[3])
print(my_array.size())
my_array.insert(3, 20)
print(my_array)
my_array.remove(31)
print(my_array)
my_array.erase(2)
my_array[0] = 50
print(my_array)
print(my_array.is_empty())
[31, 77, 17, 93] 93 4 [31, 77, 17, 20, 93] [77, 17, 20, 93] [50, 17, 93] False
A.2 Compact Array¶
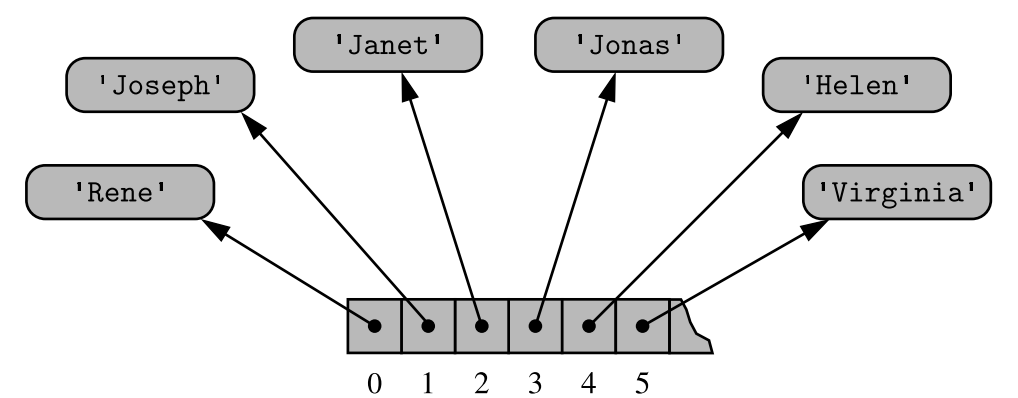
Assume that we have a list in Python, such as: ['Rene' , 'Joseph' , 'Janet' , 'Jonas' , 'Helen' , 'Virginia', ... ].
To represent such a list with an array, Python must adhere to the requirement that each cell of the array use the same number of bytes. Yet the elements are strings, and strings naturally have different lengths!
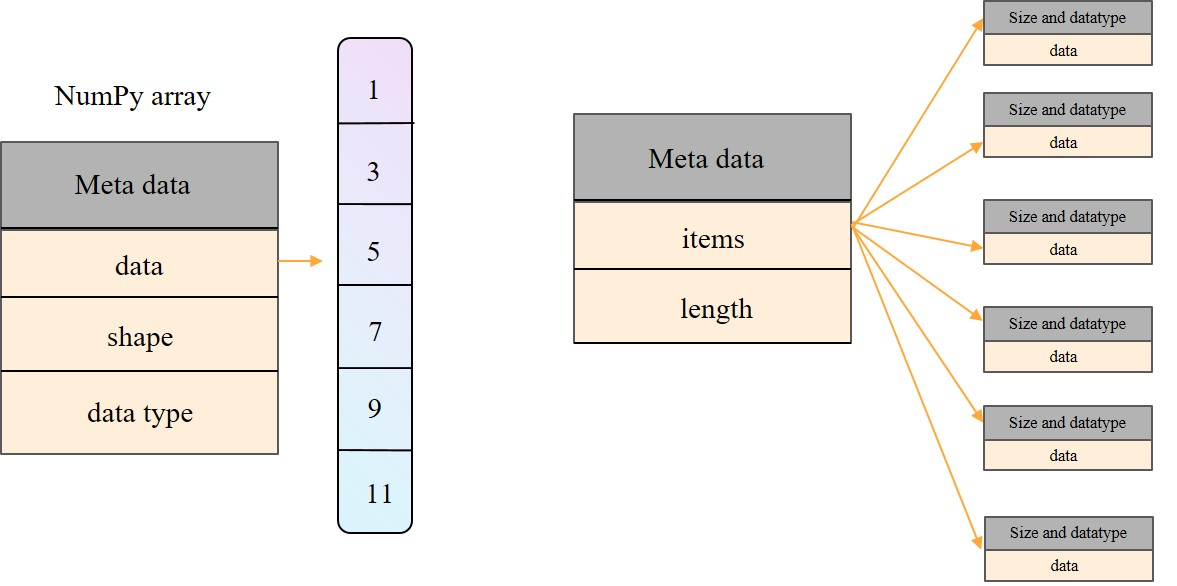
Instead, Python represents a list or tuple instance using an internal storage mechanism of an array of object references. Although the relative size of the individual elements may vary, the number of bits used to store the memory address of each element is fixed (e.g., 64-bits per address). In this way, Python can support constant-time access!
On the other hand, strings are represented using an array of characters (not an array of references). We will refer to this more direct representation as a compact array because the array is storing the bits that represent the primary data (characters, in the case of strings)!
The overall memory usage will be much lower for a compact structure because there is no overhead devoted to the explicit storage of the sequence of memory references (in addition to the primary data)!
A referential structure will typically use 64-bits for the memory address stored in the array, on top of whatever number of bits are used to represent the object! Also, each Unicode character stored in a compact array within a string typically requires 2 bytes! Python provides several means for creating compact arrays of various types. The most common used one is array from NumPy:
from numpy import array, int32, arange
primes = array([2, 3, 5, 7, 11, 13, 17, 19], dtype=int32)
primes
array([ 2, 3, 5, 7, 11, 13, 17, 19])

The public interface for the array class conforms mostly to that of a Python list. However, the constructor for the array class requires a type code. The type code, int32, designates an array of (signed) integers. The type code allows the interpreter to determine precisely how many bits are needed per element of the array!
A.3 Multidimensional Arrays¶
The arrays discussed so far are known as one-dimensional arrays because the data is organized linearly in only one direction. Many applications require that data be stored in more than one dimension. One common example is a table, which is an array that consists of rows and columns. This is commonly called a two-dimensional array (Matrix):
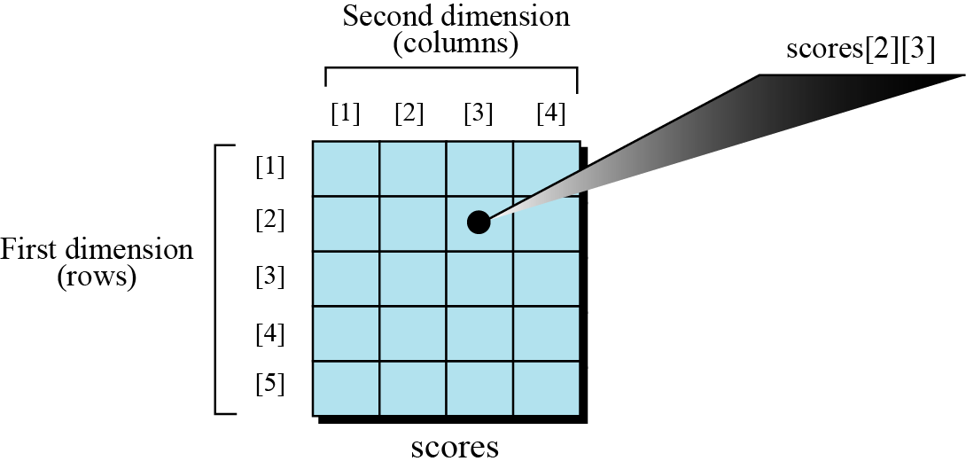
The array holds the scores of students in a class. There are five students in the class and each student has four different scores for four subjects. The variable scores[2][3] show the score of the second student in the third quiz.
Arranging the scores in a two-dimensional array can help us to find the average of scores for each student (the average over the row values) and find the average for each subject (the average over the column values) and so on. Note that multidimensional arrays — arrays with more than two dimensions — are also possible.
# a matrix: the argument to the array function is a nested Python list
M = array([[1, 1], [2, 2]], dtype=int32) # You can use nested list to implement 2D array in Python
M, type(M), M.dtype, M.shape
(array([[1, 1],
[2, 2]]),
numpy.ndarray,
dtype('int32'),
(2, 2))
Note the slicing of array works the same way as Python list!
M[0,:] # row 0
array([1, 1])
M[:,0] # column 0
array([1, 2])
M[1,1] #row1, column1
2
A.3.1 Memory layout¶
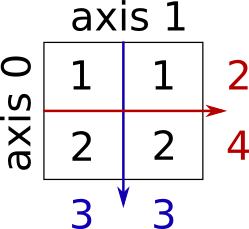
The indexes in a one-dimensional array directly define the relative positions of the element in actual memory. A two-dimensional array, however, represents rows and columns. How each element is stored in memory depends on the computer!
Most computers use row-major storage, in which an entire row of an array is stored in memory before the next row. However, a computer may store the array using column-major storage, in which the entire column is stored before the next column. The following figure shows a two-dimensional array and how it is stored in memory using row-major or column-major storage. Row-major storage is more common.
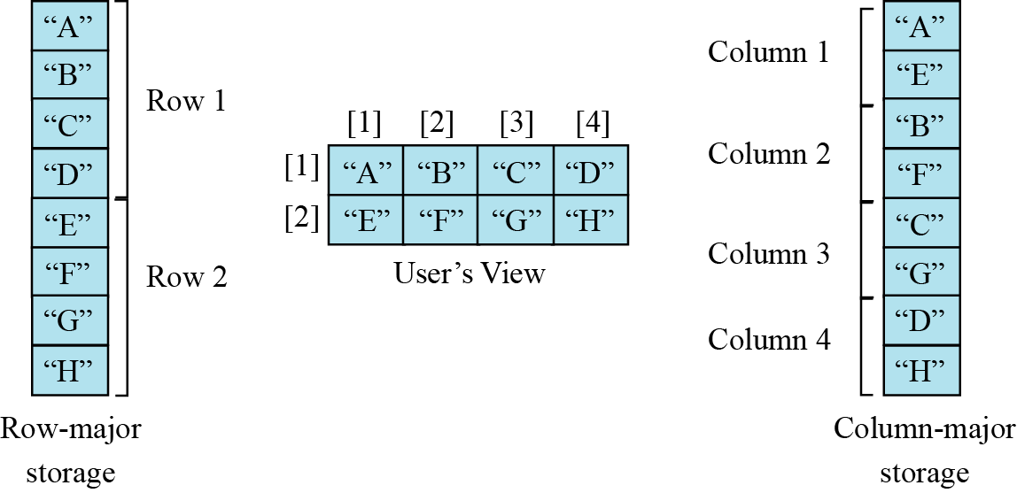
By default, array are row-major (C_CONTIGUOUS)
M.flags
C_CONTIGUOUS : True F_CONTIGUOUS : False OWNDATA : True WRITEABLE : True ALIGNED : True WRITEBACKIFCOPY : False
You can change to column major (F_CONTIGUOUS) but it will be much slower in NumPy due to the cache effect (functions in numpy assumes that the array are stored in column major)
M = array([[1, 1], [2, 2]], dtype=int32, order='F')
M.flags
C_CONTIGUOUS : False F_CONTIGUOUS : True OWNDATA : True WRITEABLE : True ALIGNED : True WRITEBACKIFCOPY : False
Exercise 1: We have stored the two-dimensional array students in the memory. The array is 100 × 4 (100 rows and 4 columns). Show the address of the element
students[5][3]assuming that the elementstudent[0][0]is stored in the memory location with address 0 and each element occupies only one memory location. The computer uses row-major storage.
import numpy as np
student = np.random.randint(0,100,size=(100,4)) #2D array
s = student.flatten() #1D array
assert student[5][3] == s[?]
We can use the following formula to find the location of an element, assuming each element occupies one memory location:
$y = x + Cols \times i + j$
where x defines the start address, Cols defines the number of columns in the array, i defines the row number of the element, j defines the column number of the element, and y is the address we are looking for!
Your answer here
A.4 Sparse Martrix¶
A sparse matrix is a matrix that has a value of 0 for most elements. If the ratio of Number of Non-Zero (NNZ) elements to the size is less than 0.5, the matrix is sparse!
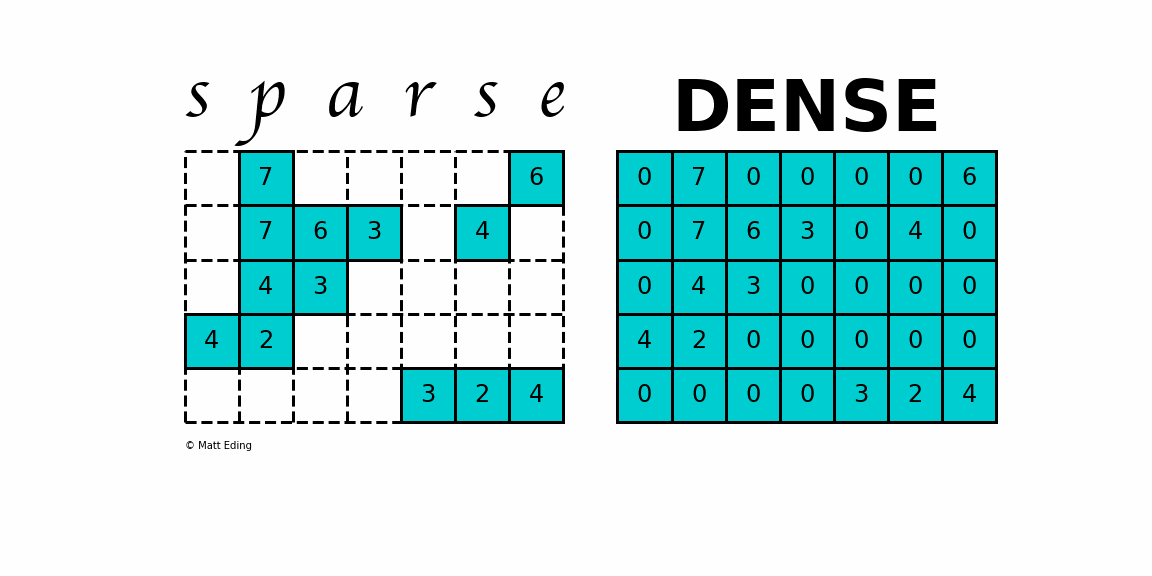
Storing information about all the 0 elements is inefficient, so we will assume unspecified elements to be 0. Using this scheme, sparse matrices can perform faster operations and use less memory than its corresponding dense matrix representation.
Different sparse formats have their strengths and weaknesses. A good starting point is looking at formats that are efficient for constructing these matrices. Typically you would start with one of these forms and then convert to another when ready to do calculations.
A.4.1 Coordinate Matrix¶
Perhaps the simplest sparse format to understand is the COOrdinate (COO) format. This variant uses three subarrays to store the element values and their coordinate positions.
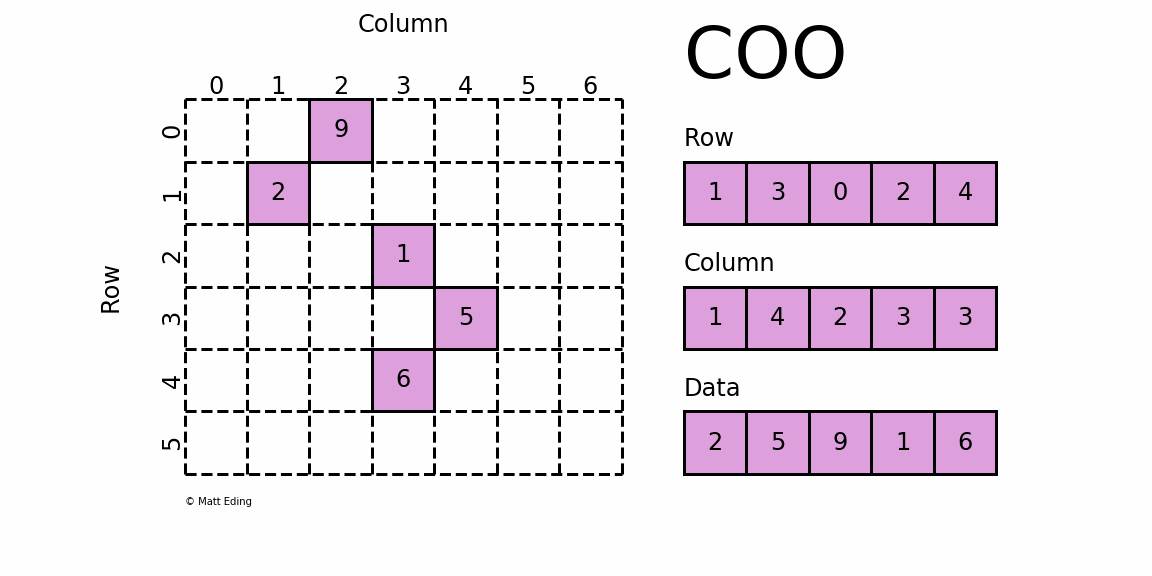
The savings on memory consumption is quite substantial as the matrix size increases. Managing data in a sparse structure is a fixed cost unlike the case for dense matrices.
The overhead incurred from needing to manage the subarrays is becomes negligible as data grows making it a great choice for some datasets!
A.4.2 Dictionary of Keys Matrix¶
Dictionary Of Keys (DOK) is very much like COO except that it subclasses dict to store coordinate-data information as key-value pairs. Since it uses a hash table as storage, identifying values at any given location has constant lookup time!
Use this format if you need the functionality that come with builtin dictionaries, but be mindful that hash tables hog more memory than arrays.
The SparseMatrix class uses a dictionary to store non-zero elements, with keys as (row, column) tuples and values as the non-zero elements.
class SparseMatrix:
"""Sparse Matrix class
Args:
data: A dictionary of (i, j) -> value
"""
def __init__(self, data = None):
self.data = data or {}
def __getitem__(self, key):
return self.data.get(key, 0)
def __setitem__(self, key, value):
self.data[key] = value
def __delitem__(self, key):
del self.data[key]
def __len__(self):
return len(self.data)
def __str__(self):
return str(self.data)
We can easily implement relational operations as follows:
def __eq__(self, other):
return self.data == other.data
def __ne__(self, other):
return self.data != other.data
def _nrows(self):
if not self.data:
return 0
max_row_index = max(key[0] for key in self.data)
return max_row_index + 1
def _ncols(self) -> int:
if not self.data:
return 0
max_col_index = max(key[1] for key in self.data)
return max_col_index + 1
The arithmetic operation is slightly more involved:
def __add__(self, other):
if self._nrows != other._nrows or self._ncols != other._ncols:
raise ValueError("Matrices must have the same dimensions for addition")
result = SparseMatrix(self._nrows, self._ncols)
for i in range(self._nrows):
for j in range(self._ncols):
result[i, j] = self[i, j] + other[i, j]
return result
def __mul__(self, other):
if self._ncols != other._nrows:
raise ValueError("Invalid dimensions for matrix multiplication")
result = SparseMatrix(self._nrows, other._ncols)
for i in range(self._nrows):
for j in range(other._ncols):
sum = 0
for k in range(self._ncols):
sum += self[i, k] * other[k, j]
result[i, j] = sum
return result
Another variant that uses the functionality of dictionary which may be faster:
def __add__(self, other):
if not isinstance(other, SparseMatrix):
raise ValueError("Addition only supports SparseMatrix instances.")
result = SparseMatrix()
keys = set(self.data.keys()) | set(other.data.keys())
for key in keys:
result[key] = self[key] + other[key]
return result
def __mul__(self, other):
if not isinstance(other, SparseMatrix):
raise ValueError("Multiplication only supports SparseMatrix instances.")
result = SparseMatrix()
# Iterate over non-zero elements in self
for (i, k) in self.data:
# Iterate over non-zero elements in other, where the column index of other matches the row index of self
for (j, l) in other.data:
if k == j:
result[i, l] += self[i, k] * other[j, l] # Note it is [i,j] not [i][j]
return result
The conversion from dense matrix can be written as follows:
def from_dense_matrix(self, matrix):
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j] != 0:
self[i, j] = matrix[i][j]
# [self[(i, j)] for i in range(len(matrix)) for j in range(len(matrix[0])) if matrix[i][j] != 0]
return self
We can play the class as follows:
import sys
sys.path.append("../pythonds3/")
from pythonds3.basic import SparseMatrix
dense_matrix = [[1, 0, 0], [0, 2, 0], [0, 0, 3]]
sparse_matrix = SparseMatrix().from_dense_matrix(dense_matrix)
print(sparse_matrix)
matrix1 = SparseMatrix({(0, 1): 1, (1, 1): 2, (2, 2): 3})
matrix2 = SparseMatrix({(1, 1): 3, (2, 2): 4})
print(matrix1 + matrix2)
print(matrix1 - matrix2)
print(matrix1 * matrix2)
{(0, 0): 1, (1, 1): 2, (2, 2): 3}
{(0, 1): 1, (2, 2): 7, (1, 1): 5}
{(0, 1): 1, (2, 2): -1, (1, 1): -1}
{(0, 1): 3, (1, 1): 6, (2, 2): 12}
matrix1, matrix2, matrix1 + matrix2, matrix1 - matrix2, matrix1 * matrix2
(SparseMatrix( [[0, 1, 0] [0, 2, 0] [0, 0, 3]] ), SparseMatrix( [[0, 0, 0] [0, 3, 0] [0, 0, 4]] ), SparseMatrix( [[0, 1, 0] [0, 5, 0] [0, 0, 7]] ), SparseMatrix( [[0, 1, 0] [0, -1, 0] [0, 0, -1]] ), SparseMatrix( [[0, 3, 0] [0, 6, 0] [0, 0, 12]] ))
A.4.3 Linear list¶
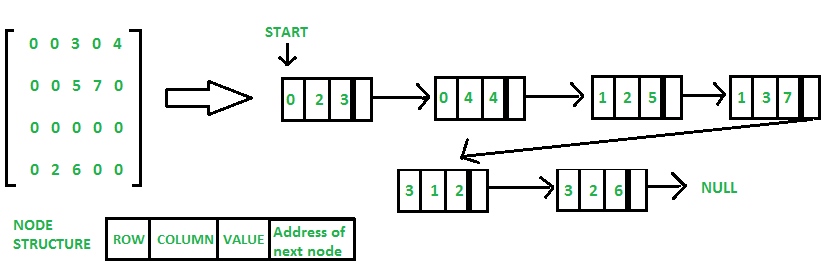
Size of array generally not predictable at time of initialization. Start with some default capacity/size (say 10). Increase capacity as needed!
References¶
Textbook 8.2.
Data Structures & Algorithms in Python Ch 5.
https://www.geeksforgeeks.org/sparse-matrix-representation/.